while循环
基本结构
while循环是C语言中最经典的循环,其一般用法为
while(循环条件)
{
循环体
}其中当循环条件满足时,执行循环体,直到条件不满足时跳出循环。
因此,我们需要定义一个循环变量,并在循环体中改变这个变量,以避免陷入死循环。
因此while循环也常常这样使用:
循环变量
while(循环条件)
{
循环体
更改循环变量
}比如下面程序
#include <stdio.h>
int main()
{
int i=0; //定义循环变量
int sum=0;
while(i<=10)
{
sum = sum + i;
i++; //改变循环变量
}
printf("sum=%d",sum);
return 0;
}这段代码计算并输出1+2+···+10的值。
练习
练习1:输出1-100中的所有素数
分析:根据素数的定义,我们可以逐个判断2~n-1能否整除n,即可写出下面代码:
#include <stdio.h>
int main()
{
int i=1;
int j=2;
printf("2\n");
while(i<=100)
{
j=2;
while(j<i)
{
if(i%j==0)
{
j++;
break;
}
if(j==i-1)printf("%d\n",i);
j++;
}
i++;
}
return 0;
}上述是判断是否为素数最直接的代码。其实,我们可以减少判断次数。
第一,j只要判断到\sqrt{i}或者说\lfloor\sqrt{i}\rfloor即可。这是因为i=\sqrt{i}\cdot\sqrt{i}=a\cdot b\ (a\leq b),由于i的因子是成对存在的,所以如果i有非1因子a,那么a\leq\sqrt{i}。
第二,所有除2的偶数也一定不是素数,这样又可以减少一部分验证。
于是,下面是改进的代码:
#include <stdio.h>
#include <math.h>
int main()
{
int i=3;
int j=2;
printf("2\n3\n");
while(i<=100)
{
j=2;
while(j<=sqrt(i))
{
if(i%j==0)
{
j++;
break;
}
if(j>sqrt(i)-1)printf("%d\n",i);
j++;
}
i=i+2;
}
return 0;
}示例输出:

练习2:输入n,并计算n!并输出
我们可以写出如下程序:
#include <stdio.h>
int main()
{
int n = 1;
int prod = 1;
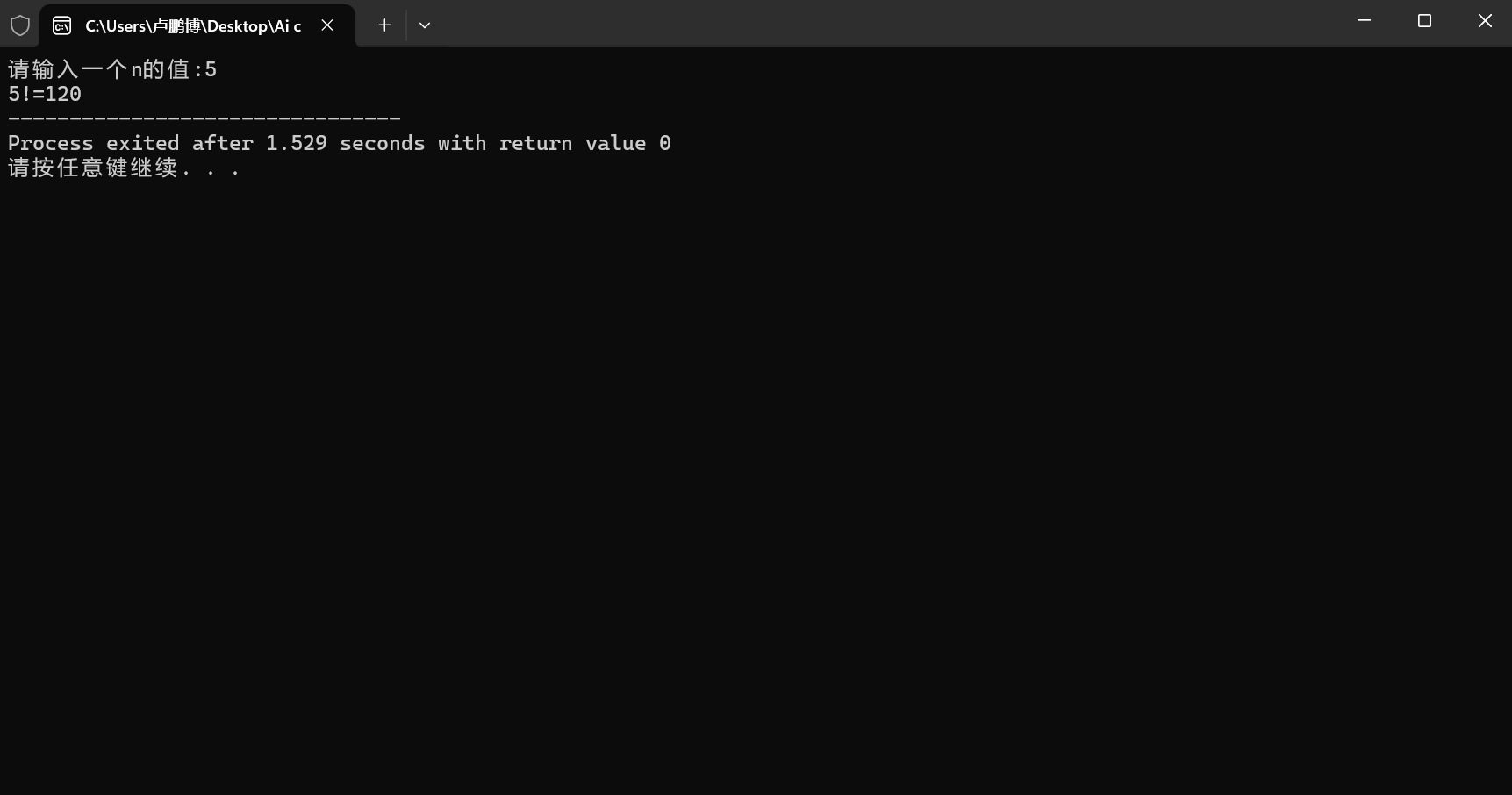
printf("请输入一个n的值:");
scanf("%d",&n);
while(n!=1)
{
prod *= n;
n--;
}
printf("%d!=%d",n,prod);
return 0;
}不过上述没有对n做出限制,如果输入的n小于0,需要提示输入数据错误。经过改进,可以得到下面代码:
#include <stdio.h>
int main()
{
int n = 1;
int prod = 1;
printf("请输入一个n的值:");
scanf("%d",&n);
while(n<0)
{
printf("输入错误!\n");
printf("请输入一个n的值:");
scanf("%d",&n);
if(n>=0)break;
}
if(n==0){printf("0!=1");return 0;}
int j=n;
while(n!=1)
{
prod *= n;
n--;
}
printf("%d!=%d",j,prod);
return 0;
}示例输出:
for循环
for循环和while循环十分类似,可以看成是简化版的while循环。for循环在明确了循环次数的循环语句中非常常用。
基本结构
for(初始循环变量,循环条件,改变循环变量)
{
循环体
}for循环比while循环更加简洁明了,不需要在外部定义循环变量。
例如下面程序,计算并输出1+2...+100的值:
#include <stdio.h>
int main()
{
int sum=0; //求和变量
for(int i;i<=100;i++) //int i这里的i变量只在for循环内起作用,如果在外部调用会报错(当然可以使用指针传递i的值)
{
sum += i;
}
printf("%d",sum);
return 0;
}于是我们可以“改造”练习一,练习二的代码如下:
练习1:
#include <stdio.h>
#include <math.h>
int main()
{
printf("2\n");
for(int i=3; i<=100; i+=2)
{
int is_prime = 1; // 假设i是素数
for(int j=2; j<=sqrt(i); j++) // 从2开始检查除数
{
if(i%j == 0)
{
is_prime = 0; // 更改i不是素数
break;
}
}
if(is_prime)printf("%d\n", i);
}
return 0;
}这里我们使用is_prime这个状态参数判断i是不是素数,先假设i是素数,方便后续调整。
练习2:
#include <stdio.h>
int main()
{
int n,prod = 1;
printf("请输入一个n的值:");
scanf("%d",&n);
while(n<0)
{
printf("输入错误!\n请输入一个n的值:");
scanf("%d",&n);
if(n>=0)break;
}
for(int i = n;i>=2;i--)
{
prod *= i;
}
printf("%d!=%d",n,prod);
return 0;
}这里我们在for循环里定义了一个临时变量i,这样,不对n做处理,可以简化0!等情况。
练习
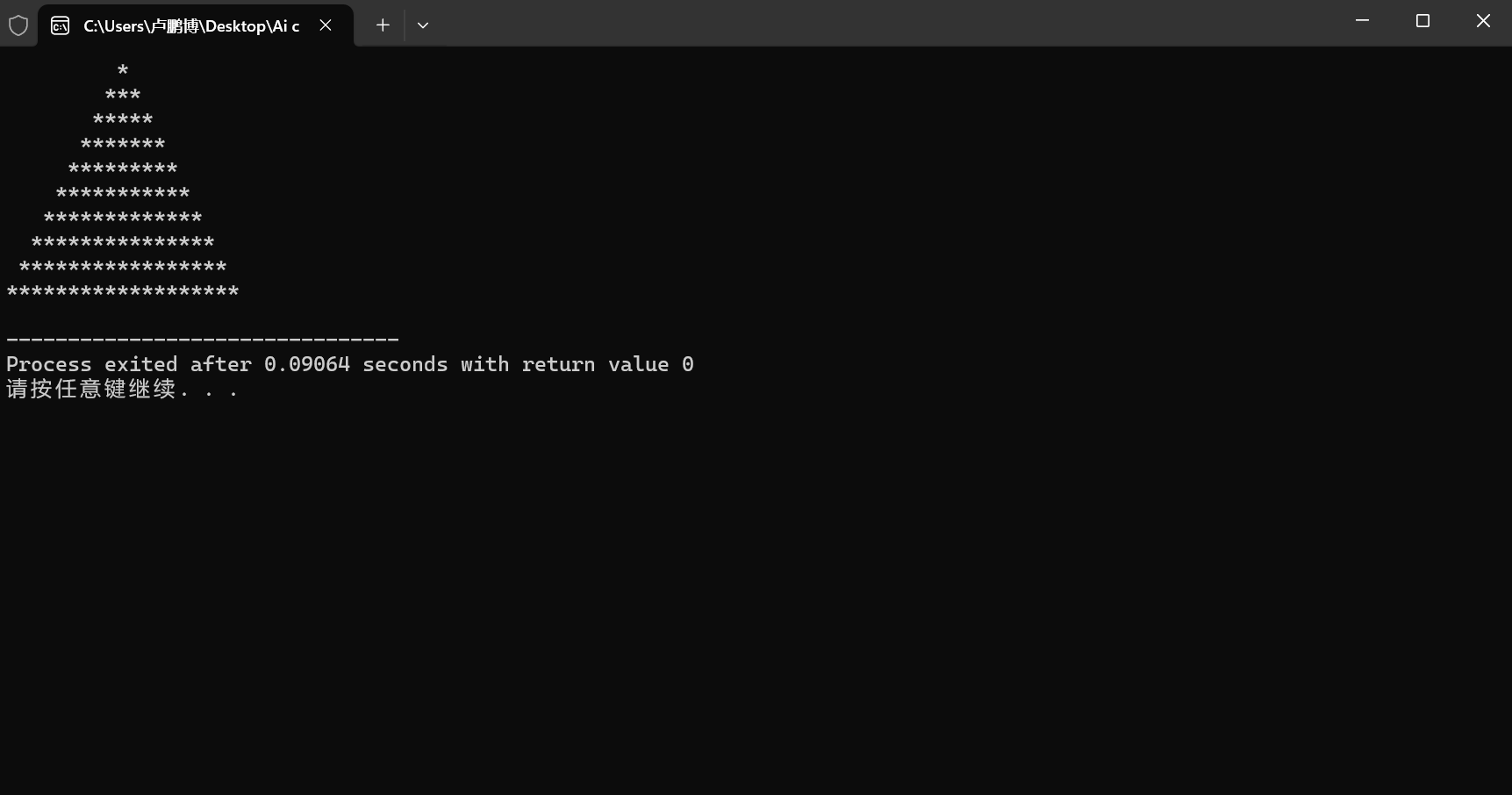
练习3:打印形如下图用*堆积的三角形

分析:我们首先需要确定输出的行数,用n表示,这里以10为例,接下来需要打印空格和*,我们采用每一行的*的个数为2i-1,那么左边空格的个数就是n-i个,这里i代表第i行。
因此在第i行时,先输出n-i个空格,即for(int j=1;j<=n-i;j++)printf(" ");
然后再输出2i-1个*即for(int j=1;j<=2*i-1;j++)printf("*");
于是可以写出下述代码:
#include<stdio.h>
int main()
{
int n=10;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n-i;j++)printf(" ");
for(int j=1;j<=2*i-1;j++)printf("*");
printf("\n");
}
return 0;
}
输出结果:
练习4:做出函数x^3-x^2-x+2的图像(该题较难,可借助ai辅助完成)
源代码:
#include <stdio.h>
#include <math.h>
// 定义函数
double f(double x) {
return x*x*x - x*x - x + 2;
}
int main() {
int width = 60; // 图形宽度
int height = 20; // 图形高度
double x_min = -2.0;
double x_max = 3.0;
double y_min = -5.0;
double y_max = 15.0;
double x_step = (x_max - x_min) / width;
double y_step = (y_max - y_min) / height;
// 计算每个点的y值
for (int row = 0; row < height; row++) {
double y = y_max - row * y_step;
for (int col = 0; col < width; col++) {
double x = x_min + col * x_step;
double y_val = f(x);
// 判断是否在函数值附近
if (fabs(y_val - y) <= y_step) {
printf("*");
} else if (fabs(y) <= y_step) { // x轴
printf("-");
} else if (fabs(x) <= x_step) { // y轴
printf("|");
} else {
printf(" ");
}
}
printf("\n");
}
// 打印坐标轴标签
printf("\n");
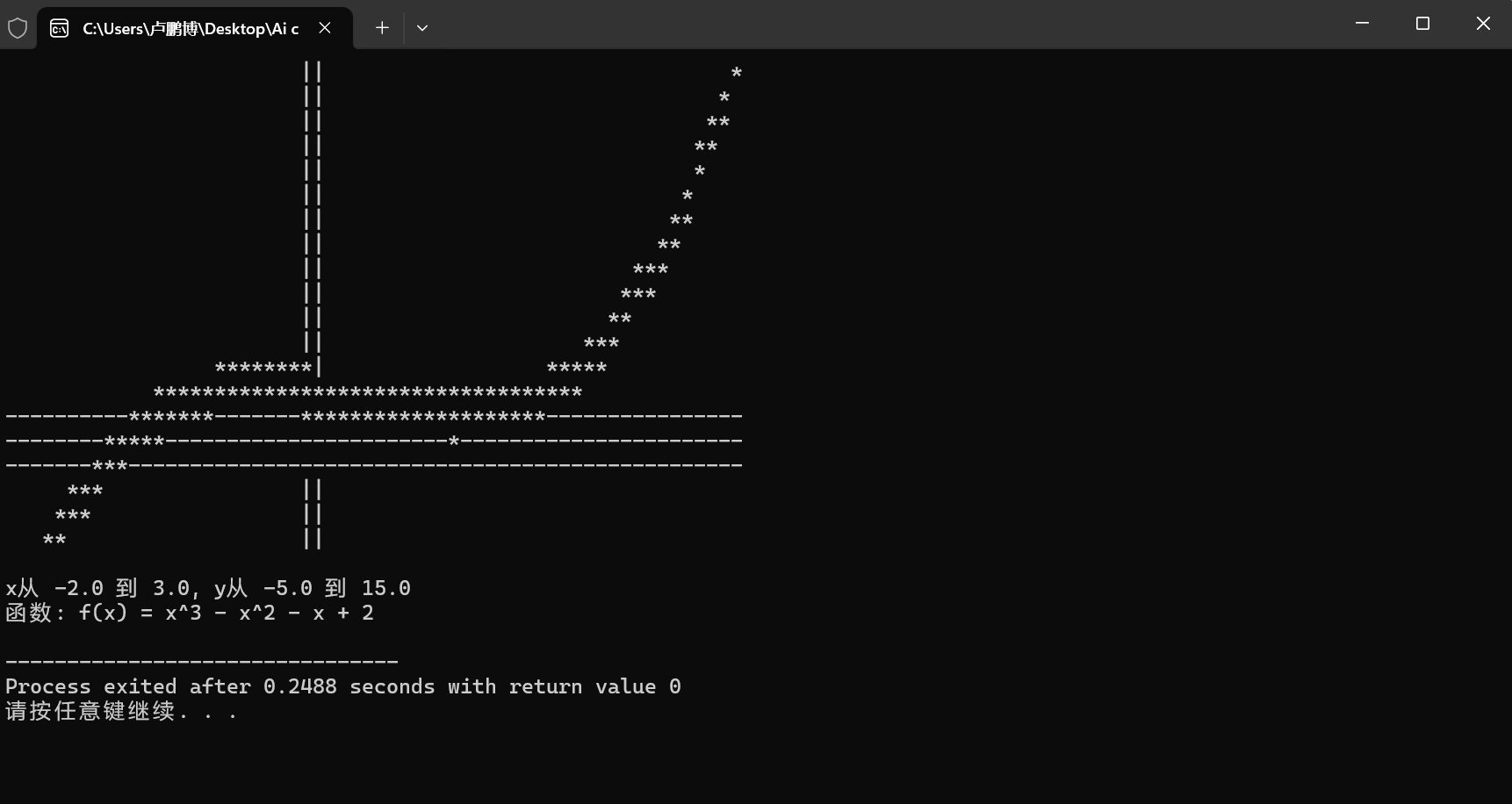
printf("x从 %.1f 到 %.1f, y从 %.1f 到 %.1f\n", x_min, x_max, y_min, y_max);
printf("函数: f(x) = x^3 - x^2 - x + 2\n");
return 0;
}输出:
while循环与for循环之间的关系
for循环是在while循环的基础上改进而来,因此for循环与while均可完成循环操作和任务。
for循环有三个参数,for(初始循环变量,循环条件,改变循环变量)
其中初始循环变量是在进入循环体之前执行一次,之后不再执行;改变循环变量是在循环体结束之后再执行,因此二者可以相互转换,二者有如下关系:
for(初始循环变量,循环条件,改变循环变量)
{
循环体
}与
初始循环变量
while(循环条件)
{
循环体
改变循环变量
}等价。
比如:
#include <stdio.h>
int main()
{
int i=0;
int sum=0;
while(i<=10)
{
sum += i;
i++;
}
printf("sum=%d",sum);
return 0;
}与
#include <stdio.h>
int main()
{
int sum=0;
for(int i=0;i<10;i++)
{
sum += i;
}
printf("sum=%d",sum);
return 0;
}等价。
do...while循环
基本结构
do...while循环和while循环类似,只是运行的初值不同,其基本结构为:
do
{
循环体
}
while(循环条件);为了防止死循环,一般使用如下格式:
定义循环变量
do
{
循环体
改变循环条件
}
while(循环条件);特点
do...while的特点是,无论循环条件是否满足,先执行一遍循环体,再判断是否满足循环条件。如果条件满足,则继续循环,如果条件不满足,则停止循环。
与while循环的转换
定义循环变量
do
{
循环体
改变循环条件
}
while(循环条件);与
定义循环变量
循环体 //执行1次
改变循环条件 //执行1次
while(循环条件)
{
循环体
改变循环条件
}例如
#include <stdio.h>
int main()
{
int i = 5;
i--;
printf("%d\n",i);
while(i)
{
i--;
printf("%d\n",i);
}
return 0;
}与
#include <stdio.h>
int main()
{
int i = 5;
do
{
i--;
printf("%d\n",i);
}while(i);
return 0;
}完全等价。
这样,我们可以把练习2的代码进行修改。
练习二修改后的代码:
#include <stdio.h>
int main()
{
int n,prod = 1;
do
{
if(n<0)printf("输入错误!\n");
printf("请输入一个n的值:");
scanf("%d",&n);
if(n>=0)break;
}while(n<0);
for(int i = n;i>=2;i--)
{
prod *= i;
}
printf("%d!=%d",n,prod);
return 0;
}练习
练习5:使用牛顿迭代法计算x^3-x^2-x+2=0的近似解(该方程仅有一个根)。
提示:迭代公式为:
分析:我们可以选定一个误差e,当|x_{n+1}-x_{n}|<e 即认为x_{n+1}满足精度要求并输出其值。{f^{'}(x)}=3x^2-2x-1
首先我们可以确定其解在[-2,-1]之间,故可取x_0=-1进行迭代。
故可写出如下代码:
#include <stdio.h>
int main()
{
double x,y=-1;
double e=0.01;
do
{
y = x;
x = x-(x*x*x-x*x-x+2)/(3*x*x-2*x-1);
if(x-y<=e&&y-x<=e)break;
}while(1); //一直循环,直到满足条件跳出循环
printf("近似解为x=%lf",x);
return 0;
}输出为:
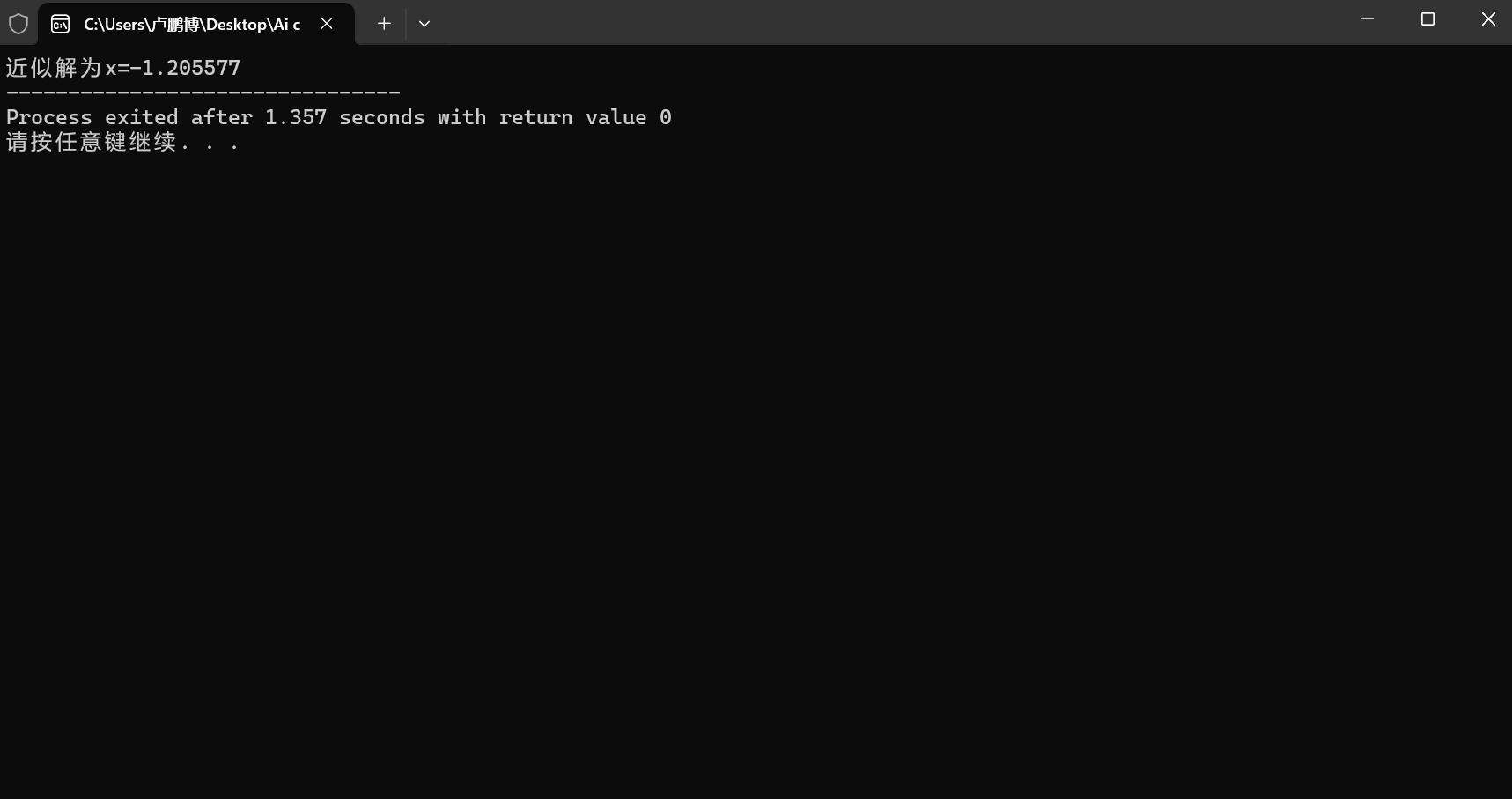
这与真实解x=-1.205569430...非常接近。
如果想要提升精度,一方面可以将上述结果重新赋予x,y进行迭代,另一方面需要减小e的值,并增加输出的小数位数(比如%.10f)。